Прогнозирование в Excel
Опубликовано 20 Июл 2014
Рубрика: Справочник Excel | 8 комментариев
 Аппроксимация функции нескольких независимых переменных (множественная регрессия) – очень интересная, имеющая огромное практическое значение задача! Если научиться ее решать, то можно стать почти волшебником, умеющим делать очень достоверные прогнозы...
Аппроксимация функции нескольких независимых переменных (множественная регрессия) – очень интересная, имеющая огромное практическое значение задача! Если научиться ее решать, то можно стать почти волшебником, умеющим делать очень достоверные прогнозы...
...результатов различных процессов на основе данных предыдущих периодов времени. В этой статье мы рассмотрим прогнозирование в Excel при помощи очень мощного и удобного инструмента — встроенных статистических функций ЛИНЕЙН и ЛГРФПРИБЛ.
Не пугайтесь «умных» терминов! Все, на самом деле, не так страшно, как кажется вначале! Не пожалейте время и прочтите эту статью внимательно до конца. Умение применять на практике эти функции существенно увеличит ваш «вес» как специалиста в глазах коллег, руководителей и в своих собственных глазах!
В одной из самых популярных статей этого блога подробно рассказано об аппроксимации функции одной переменной в Excel (рекомендую прочесть). Но в реальных жизненных процессах результат, как правило, зависит от многих независимых друг от друга факторов (переменных). Как выявить и учесть все эти факторы, связать их воедино и на основании накопленных статистических данных спрогнозировать расчетный конечный результат для некоего нового набора исходных параметров? Как оценить достоверность прогноза и степень влияния на результат каждой из переменных? Ответы на эти и другие вопросы – далее в тексте статьи.
Что можно научиться прогнозировать? Очень многое! В принципе, можно научиться прогнозировать любые самые разнообразные результаты процессов в повседневной жизни и работе. Всегда, когда возникает вопрос: «А что будет, если…?» зовите на помощь Excel, рассчитывайте прогноз и проверяйте его достоверность!
Можно научиться прогнозировать зависимость прибыли от цены и объемов продаж любого товара.
Можно научиться прогнозировать зависимость цены автомобилей на вторичном рынке от марки, мощности, комплектации, года выпуска, количества предыдущих владельцев, пробега.
Можно научиться устанавливать зависимость объемов продаж товаров от затрат на различные виды рекламы.
Можно научиться выполнять прогнозирование в Excel стоимости наборов любых услуг в зависимости от их состава и качества.
В производстве, используя косвенные простые параметры, можно научиться прогнозировать трудоемкость и объем выпускаемой продукции, потребление материалов и энергоресурсов, и т.д.
Прежде чем начать решать практическую задачу, хочу обратить внимание на один весьма важный момент. Научиться выполнять прогнозирование в Excel с использованием вышеназванных функций ЛИНЕЙН и ЛГРФПРИБЛ технически не очень сложно. Гораздо сложнее научиться анализировать процесс, приводящий к результату и находить простые факторы, влияющие на него. При этом желательно (но не обязательно) понимать — КАК зависит результат (функция) от каждого из факторов (переменных). Линейная это зависимость или может быть степенная или какая-нибудь другая? Понимание физического смысла процесса поможет вам правильно выбрать переменные. Подбор аппроксимирующей функции следует производить при полном понимании логики и смысла процесса, приводящего к результату.
Подготовка к прогнозированию в Excel.
1. Четко формулируем название и единицу измерения интересующего нас результата процесса. Это и есть искомая функция — y, аналитическое выражение которой мы будем определять с помощью MS Excel.
В примере, представленном чуть ниже, y— это срок изготовления заказа в рабочих днях.
2. Производим анализ процесса и выявляем факторы — аргументы функции — x1, x2, ... xn — наиболее сильно на наш взгляд влияющие на результат – значения функции y. Внимательно назначаем единицы измерений для переменных.
В примере это:
x1 — суммарная длина всех прокатных профилей в метрах, из которых изготавливается заказ
x2 — общая масса всех прокатных профилей в килограммах
x3 — суммарная площадь всех листов в метрах квадратных
x4 — общая масса всех листов в килограммах
3. Собираем статистику – фактические данные – в виде таблицы.
В примере – это фактические данные о металлопрокате и фактических сроках выполненных ранее заказов.
Очень важно при выборе переменных x1, x2, ... xn учесть их доступность. То есть, значения этих факторов должны быть у вас в виде достоверных статистических данных. Очень желательно, чтобы получение значений статистических данных было простым, понятным и нетрудоемким процессом.
Прогнозирование в Excel сроков изготовления заказов.
Переходим непосредственно к рассмотрению примера.
Небольшой участок завода производит строительные металлоконструкции. Входным сырьем является листовой и профильный металлопрокат. Мощность участка в рассматриваемом периоде времени неизменна. В наличии есть статистические данные о сроках изготовления 13-и заказов (k=13) и количестве использованного металлопроката. Попробуем найти зависимость срока изготовления заказа от суммарной длины и массы профильного проката и суммарной площади и массы листового проката.
В рассмотренном примере срок изготовления заказа напрямую зависит от мощности производства (люди, оборудование) и трудоемкости выполнения технологических операций. Но детальные технологические расчеты очень трудоемки и, соответственно, длительны и дороги. Поэтому в качестве аргументов функции выбраны четыре параметра, которые легко и быстро можно посчитать при наличии спецификации металлопроката, и которые косвенно влияют на результат – срок изготовления. В результате анализа была установлена сильнейшая связь между изменениями исходных данных и результатами процесса изготовления металлоконструкций.
Примечательно, что найденная зависимость связывает в одной формуле параметры с различными единицами измерения. Это нормально. Найденные коэффициенты не являются безразмерными. Например, размерность коэффициента b – рабочие дни, а коэффициента m1– рабочие дни/м.
1. Запускаем MS Excel и заполняем ячейки B4...F16 таблицы Excel исходными статистическими данными. В столбцы пишем значения переменных xi и фактические значения функции y, располагая данные, относящиеся к одному заказу в одной строке.

2. Так как функции ЛИНЕЙН и ЛГРФПРИБЛ — функции выводящие результаты в виде массива, то их ввод имеет некоторые особенности. Выделяем область размером 5×5 ячеек — ячейки I9...M13. Количество выделенных строк всегда — 5, а количество столбцов должно быть равно количеству переменных xi плюс 1. В нашем случае это: 4+1=5.
3. Нажимаем на клавиатуре клавишу F2 и набираем формулу
в ячейках I9...M13: =ЛИНЕЙН(F4:F16;B4:E16;ИСТИНА;ИСТИНА)
4. После набора формулы необходимо для ее ввода нажать сочетание клавиш Ctrl+Shift+Enter. (Знак «+» нажимать не нужно, в записи он означает, что клавиши нажимаются последовательно при удержании нажатыми всех предыдущих.)
5. Считываем результаты работы функции ЛИНЕЙН в ячейках I9...M13.
Карту, поясняющую значения каких параметров в каких ячейках выводятся, я расположил в ячейках I4...M8 для удобства чтения сверху над массивом значений.
Общий вид уравнения аппроксимирующей функции y, представлен в объединенных ячейках I2...M2.
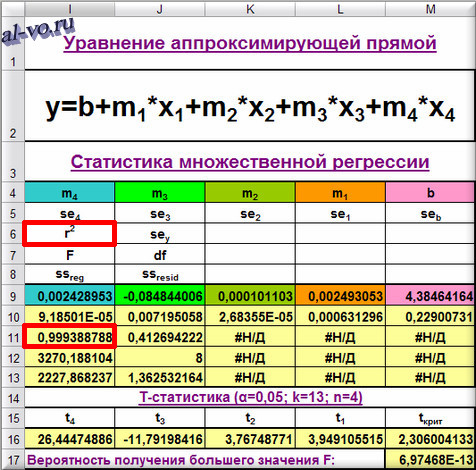
Значения коэффициентов b, m1, m2, m3, m4 считываем соответственно
в ячейке M9: b=4,38464164
в ячейке L9: m1=0,002493053
в ячейке K9: m2=0,000101103
в ячейке J9: m3=-0,084844006
в ячейке I9: m4=0,002428953
6. Для определения расчетных значений функции y — срока изготовления заказа — вводим формулу
в ячейку G4: =$L$9*B4+$K$9*C4+$J$9*D4+$I$9*E4+$M$9 =5,0
y=b+m1*x1+m2*x2+m3*x3+m4*x4
7. Копируем эту формулу во все ячейки столбца от G5 до G17 «протягиванием» и сверяем расчетные значения с фактическими. Совпадение очень хорошее!
8. Предварительные действия все выполнены. Уравнение аппроксимирующей функции y найдено. Пробуем выполнить прогнозирование в Excel срока изготовления нового заказа. Вписываем исходные данные.
8.1. Длину прокатных профилей по проекту x1 в метрах пишем
в ячейку B17: 2820
8.2. Массу прокатных профилей x2 в килограммах пишем
в ячейку C17: 62000
8.3. Площадь листового проката, используемого в новом заказе по проекту, x3 в метрах квадратных заносим
в ячейку D17: 110,0
8.4. Общую массу листового проката x4 в килограммах вписываем
в ячейку E17: 7000
9. Расчетный срок изготовления заказа y в рабочих днях считываем
в ячейке G17: =$L$9*B17+$K$9*C17+$J$9*D17+$I$9*E17+$M$9 =25,4
Прогнозирование в Excel выполнено. На основе статистических данных мы рассчитали предположительный срок выполнения нового заказа — 25,4 рабочих дней. Остается выполнить заказ и сверить фактическое время с прогнозным.
Анализ результатов.
Мы не будем погружаться глубоко в дебри статистических терминов и расчетов, но некоторых практических аспектов все же придется коснуться.
Обратимся к другим данным в массиве, которые вывела функция ЛИНЕЙН.
Во второй строке массива в ячейках I10…M10 выведены стандартные ошибки se4, se3, se2, se1, seb для расположенных выше в первой строке массива соответствующих коэффициентов уравнения аппроксимирующей функции m4, m3, m2, m1, b.
В третьей строке в ячейке I11 выведено значение коэффициента множественной детерминации r2, а в ячейке J11 — стандартная ошибка для функции — sey.
В четвертой строке в ячейке I12 находится, так называемое F-наблюдаемое значение, а в ячейке J12 — df – количество степеней свободы.
Наконец, в пятой строке в ячейках I13 и J13 соответственно размещены ssreg — регрессионная сумма квадратов и ssresid — остаточная сумма квадратов.
На что следует в регрессионной статистике обратить особое внимание? Что для нас наиболее важно?
1. На сколько достоверно прогнозирует срок изготовления полученное уравнение функции y? При высокой достоверности аппроксимации значение коэффициента детерминации r2 близко к максимуму — к 1! Если r2<0,7…0,8, то различия между фактическими и расчетными значениями функции будут значительными, и применять полученную формулу для прогнозирования, скорее всего, нельзя.
В нашем примере r2=0,999388788. Это означает, что найденное уравнение функции y чрезвычайно точно определяет срок изготовления заказа по четырем входным данным. Вышесказанное подтверждается сравнительным анализом значений в ячейках F4…F16 и G4…G16 и указывает на существенную зависимость между сроком изготовления и данными о входящем в заказ металлопрокате.
2. Определим важность и полезность каждой из четырех переменных x1, x2, x3, x4 в полученной формуле с помощью, так называемой, t-статистики.
2.1. Рассчитываем t4, t3, t2, t1, соответственно
в ячейке I16: t4 =I9/I10 =26,44474886
в ячейке J16: t3 =J9/J10 =-11,79198416
в ячейке K16: t2 =K9/K10 =3,76748771
в ячейке L16: t1 =L9/L10 =3,949105515
ti=mi/sei
2.2. Вычисляем двустороннее критическое значение tкрит с уровнем достоверности α=0,05 (предполагается 5% ошибок) и количеством степеней свободы df=8
в ячейке M16: tкрит =СТЬЮДРАСПОБР(0,05; J12) =2,306004133
Так как для всех ti справедливо неравенство |ti|>tкрит, то это означает, что все выбранные переменные xi полезны при расчете сроков изготовления заказов – y.
Наиболее значимой переменной при прогнозировании в Excel сроков изготовления заказов y является x4, так как |t4|>|t3|>|t1|>|t2|.
3. Не является ли случайным полученное значение коэффициента детерминации r2? Проверим это, используя F-статистику (распределение Фишера), которая характеризует «неслучайность» высокого значения коэффициента r2.
3.1. F-наблюдаемое значение считываем
в ячейке I12: 3270,188104
3.2. F-распределение имеет степени свободы v1 и v2.
v1=k— df-1=13-8-1=4
v2=df=8
Рассчитаем вероятность получения значения F-распределения большего, чем F-наблюдаемое
в ячейке I12: =FРАСП(I12;4;J12) =6,97468*10-13
Так как вероятность получения большего значения F-распределения, чем наблюдаемое чрезвычайно мала, то из этого следует вывод — найденное уравнение функции y можно применять для прогнозирования сроков изготовления заказов. Полученное значение коэффициента детерминации r2 не является случайным!
Заключение.
Применение функции MS Excel ЛГРФПРИБЛ почти не отличается от работы с функцией ЛИНЕЙН кроме вида уравнения искомой функции, которое принимает для рассмотренного примера следующий вид:
y=b*(m1x1)*(m2x2)*(m3x3)*(m4x4)
Статистика множественной регрессии, которую рассчитывает функция ЛГРФПРИБЛ, базируется на линейной модели:
ln (y)=x1*ln (m1)+x2*ln (m1)...+xn*ln (mn)+ln (b)
Это означает, что значения, например, sei нужно сравнивать не с mi, а с ln (mi). (Подробнее об этом почитайте в справке MS Excel.)
Если в результате использования функции ЛГРФПРИБЛ коэффициент детерминации r2 окажется ближе к 1, чем при использовании функции ЛИНЕЙН, то применение аппроксимирующей функции вида
y=b*(m1x1)*(m2x2)…*(mnxn),
несомненно, является более целесообразным.
Если прогнозное значение функции y находится вне интервала фактических статистических значений y, то вероятность ошибки прогноза резко возрастает!
Для обеспечения высокой точности прогнозирования в Excel необходима точная и обширная статистическая база данных – информация об известных из практики результатах процессов. Но, даже имея в наличии такую базу, вы не будете застрахованы от ложных предположений и выводов. Процесс прогнозирования коварен и полон неожиданностей! Помните об этом всегда! Глубже вникайте в суть прогнозируемого процесса. Тщательней относитесь к выбору и назначению переменных. На полученные результаты всегда смотрите через «очки скептика». Такой подход поможет избежать серьезных ошибок в важных вопросах.
Ссылка на скачивание файла: prognozirovaniye-v-excel (xls 46,5KB).
Статьи с близкой тематикой
Отзывы
8 комментариев на «Прогнозирование в Excel»
Ваш отзыв
Очень полезная статья, спасибо! Искал в удобоваримом виде информацию по аппроксимации функции двух переменных, а тут наглядно и с объяснениями полученных значений.
Спасибо, подпишусь
ниче не понял, но подпишуся
Давно уже таким не занимаюсь. Тем не менее. Если тренд описывается гармонической функцией. Тренд в пределах периода. Т.е. Вы видите часть функции (например,полпериода синусоиды). Как представляете прогноз? Только без аппроксимации этого участка полиномом. Точность нужна высокая
По половине периода высокую точность прогноза, думаю, не получить.
А вообще для периодической функции, удовлетворяющей условиям Дирихле и заданной точками в равноотстоящих узлах по оси X, следует применить аппроксимацию рядом Фурье.
Так в свое время я делал с графиком уравнения времени.
Спасибо! Хотелось узнать а на площадь есть линейный раскрой в excel.
Линейный раскрой он потому и линейный, что одномерный. Раскрой площади — двумерная задача. Я не занимался этим вопросом, но решения в excel встречал в Интернете.
(Николай, Вы не в той ветке задали вопрос.)
Спасибо Вам за познавательную статью. Все доходчиво и понятно.
Спасибо за статью. Очень полезная.