Линейный раскрой в Excel
Опубликовано 02 Дек 2015
Рубрика: Справочник Excel | 49 комментариев
 Экономичный линейный раскрой материалов (раскрой погонажа) актуален для многих отраслей производства и в строительстве. Это — распил бревен и досок в деревообработке, резка прутков, арматурных стержней, уголков, швеллеров, труб, двутавров на заготовки...
Экономичный линейный раскрой материалов (раскрой погонажа) актуален для многих отраслей производства и в строительстве. Это — распил бревен и досок в деревообработке, резка прутков, арматурных стержней, уголков, швеллеров, труб, двутавров на заготовки...
...в производстве металлоконструкций и машиностроении, поперечный раскрой рулонов с бумагой и тканью в целлюлозной и легкой промышленности.
Не смотря на кажущуюся простоту, решение задач линейного раскроя является весьма не легким, но стоящим делом. Внедрение научного подхода к раскрою погонажных материалов позволяет снизить расходы на них иногда более чем на 10%! Дочитайте статью до конца и убедитесь в правоте этих слов.
Рассматриваемая тема относится к задачам линейного программирования. Для решения таких задач ученые в последние 70 лет придумали несколько различных методов.
Метод индексов Л.В. Канторовича и В.А. Залгаллера при определенном навыке позволяет «вручную» без использования вычислительной техники эффектно выполнять линейный раскрой. Любопытным читателям рекомендую с этим методом ознакомиться, прочитав книгу вышеназванных авторов «Рациональный раскрой промышленных материалов».
Симплекс-метод, основанный на идеях Л.В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века. Надстройка MS Excel «Поиск решения» (Solver) использует этот алгоритм. Именно с помощью этого метода и Excel мы будем в этой статье решать задачу линейного раскроя.
Позже появились и получили развитие генетический, жадный и муравьиный алгоритмы. Однако, ограничимся их перечислением и перейдем к делу, не забираясь в дебри теорий (хотя там, «в дебрях», очень интересно).
Включим Excel и на простом примере порезки металлических стержней на детали познакомимся с одним из способов решения практических задач линейного раскроя. Часто математики эту задачу называют «задачей о распиле».
Исходные данные для примера я не стал придумывать, а взял из статьи Покровского М.А. «Минимизация неизбежных потерь материалов в промышленном производстве при их раскрое на штучные заготовки» опубликованной в №5 (май 2015) электронного научно-технического журнала «Инженерный вестник» издаваемого ФГБОУ ВПО «МГТУ им. Н.Э. Баумана» (ссылка: engbul.bmstu.ru/doc/775784.html).
Цель, которую я преследовал – сравнить полученные результаты решения задачи.
Пример решения задачи линейного раскроя в MS Excel.
Договоримся, что:
1. Заготовки – это исходный материал в виде прутков, полос, стержней и т.д. одинаковой длины.
2. Детали – это элементы, которые необходимо получить, разрезав исходные заготовки на части.
3. Ширина пила, реза, руба принята равной нулю.
Условие задачи:
Для комплектации одного из заказов заготовительный участок должен порубить на комбинированных ножницах из одинаковых прутков-заготовок длиной 1500 мм три типоразмера деталей:
151 штуку длиной 330 мм
206 штук длиной 270 мм
163 штуки длиной 190 мм
Требуется найти оптимальный план раскроя, использующий минимальное количество материала и дающий, соответственно, минимальное количество отходов.
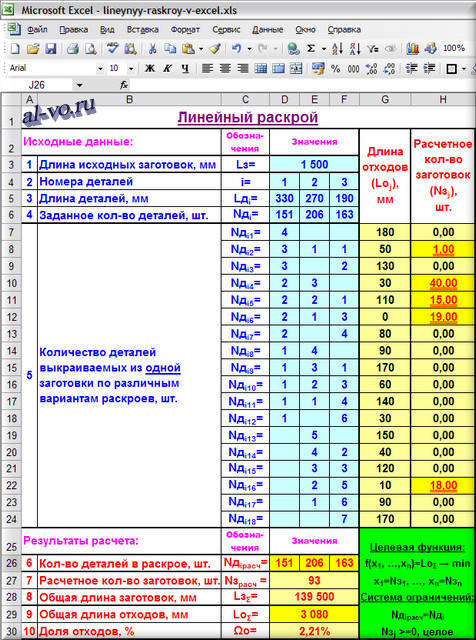
Исходные данные:
1. Длину исходных заготовок Lз в миллиметрах записываем в объединенную ячейку
D3E3F3: 1500
2. Присваиваем номера i всем типоразмерам деталей, начиная от самой длинной и заканчивая самой короткой в ячейках
D4; E4; F4: 1; 2; 3
3. Длины деталей Lдi в миллиметрах пишем в
D5; E5; F5: 330; 270; 190
4. Количество деталей Nдi в штуках заносим в
D6; E6; F6: 151; 206; 163
5.Приступаем к очень важному этапу – заполнению вариантов раскроев.
Необходимо запомнить и понять 2 принципа выполнения этой работы.
1. Длины отходов должны быть меньше самой маленькой детали (0<Loj<Lдmin).
2. «Укладку» деталей в заготовку начинаем с самых больших деталей и с самого большого их количества, последовательно двигаясь в сторону уменьшения.
Если какого-нибудь типоразмера деталей в варианте раскроя нет, то ячейку оставляем пустой, ноль писать не будем для облегчения визуального восприятия таблицы.
Вариант раскроя №1:
Попытка выкроить из одной заготовки 5 деталей №1 невозможна, поэтому пишем в ячейку
D7: 4
Добавить в раскрой деталь №2 или деталь №3 также невозможно, поэтому оставляем пустыми ячейки
E7 и F7:
Вариант раскроя №2:
Уменьшаем на 1 от предыдущего варианта количество деталей №1 и записываем в
D8: 3
Пробуем добавить 2 детали №2 – не получается, поэтому дополняем в
E8: 1
Остается возможность дополнить раскрой деталью №3. Заносим в
F8: 1
Придерживаясь озвученных принципов, заполняем по аналогии все возможные в данном случае 18 вариантов раскроев.
Сделав пару-тройку таблиц вариантов раскроев самостоятельно, вы уясните логику действий и будете тратить считанные минуты на эту работу.
Если при раскрое не выполняется первый принцип, то ячейка с длиной отхода автоматически окрашивается в красный цвет. Условное форматирование, примененное к ячейкам G7…G24, наглядно поможет вам в этой работе.
В ячейках H7…H24 ничего не пишем! Они используются для вывода результата решения!
Ссылка на скачивание файла с примером: lineynyy-raskroy-v-excel (xls 38,5KB).
Подготовка к решению:
* В ячейках G7…G24 вычисляются длины отходов (обрезков), остающиеся в результате выполнения раскроев, по формуле
Loj=Lз— Σ(Lдi*Nдij)
6. Количество деталей каждого типоразмера, изготовленных по всем примененным вариантам раскроя, будут подсчитываться в ячейках D26, E26 и F26 по формуле
Nдiрасч=Σ(Nдij*Nзj)
Количество деталей в найденном в конце решения плане раскроя должно полностью соответствовать заданному количеству деталей!
7. Необходимое число заготовок для выполнения оптимального плана раскроя будет определяться в объединенной ячейке D27E27F27 по формуле
Nзрасч=ΣNзj
8. Общая длина всех заготовок, необходимых чтобы выполнить линейный раскрой всех деталей будет подсчитываться в объединенной ячейке D28E28F28 по формуле
LзΣ= Lз*Nзрасч
9. Общая длина всех отходов, получаемых при выполнении найденного плана раскроя, будет считаться в объединенной ячейке D29E29F29 по формуле
LоΣ= Σ(Lоj*Nзj)
10. Доля отходов, полученных при выполнении оптимального плана линейного раскроя от общего количества использованного материала, будет вычисляться в объединенной ячейке D30E30F30 по формуле
Ωo= LоΣ/LзΣ
Решение:
Подготовка завершена, определены 18 вариантов наиболее оптимальных раскроев одной заготовки на детали и вписаны все необходимые формулы. Теперь предстоит решить главную задачу: определить оптимальный план раскроя – сколько заготовок, и по каким вариантам раскроев резать, чтобы в итоге получить все необходимые детали в нужном количестве при минимуме отходов.
1. Выбираем в главном меню «Сервис» - «Поиск решения…».
2. В появившемся одноименном окне «Поиск решения» производим настройки.
2.1. Назначаем целевой функцией общую длину отходов LоΣ и вводим ссылку в окно целевой ячейки.
2.2. Устанавливаем переключатель «Равной:» в положение «минимальному значению».
2.3. Указываем ячейки с переменными Nзj в окне «Изменяя ячейки».
2.4. Вводим ограничения в одноименное окно. В качестве условий указываем необходимость равенства заданного Nдi и расчетного Nдiрасч количества деталей, а так же на переменные Nзj – расчетное количество заготовок по вариантам раскроев – накладываем ограничение: это должны быть целые числа.

3. Нажимаем кнопку «Параметры» и в выпавшем окне «Параметры поиска решения» выполняем настройки так, как показано на следующем скриншоте. Закрываем окно кнопкой «ОК».

4. В окне «Поиск решения» нажимаем кнопку «Выполнить» и ждем, пока Excel найдет решение. Это может длиться несколько минут.

5. После сохранения найденного решения кнопкой «ОК», результаты отобразятся в ячейках H7...H24 на листе Excel.
На следующей картинке показан найденный оптимальный линейный раскройный план.

Что в итоге?
Линейный раскрой в Excel заготовок для задач подобных рассмотренной в этой статье выполняется описанным выше методом за 10-15 минут! «Вручную», не зная метод индексов Канторовича, за такое время решения не найдешь.
Запустив «Поиск решения» несколько раз при разных параметрах поиска, удалось найти 5 различных планов рубки заготовок. Все 5 планов требуют одинаковое число заготовок – 93 и дают отходов всего 2,21%!!! Эти планы почти на 6% лучше, чем план, рассчитанный Покровским и более чем на 10% экономичнее «Традиционного» плана (смотри ссылку на первоисточник в первой части статьи). Очень достойный результат достигнут быстро и без применения дорогостоящих программ.

Следует заметить, что надстройка Excel Solver («Поиск решения»), использующая симплекс-метод при решении задач линейного программирования, может работать не более чем с 200 переменными. В приложении к рассмотренной нами задаче линейного раскроя это означает, что количество раскроев не может превышать 200 вариантов. Для простых задач этого достаточно. Для более сложных задач следует попробовать применить «смесь» «жадного» алгоритма и симплексного метода Solver, отобрав из полного списка раскроев не более 200 самых экономичных. Далее запасаемся терпением и добиваемся результатов. Можно попытаться разбить сложную задачу на несколько простых, но «уровень оптимальности» найденного решения будет при этом, скорее всего, ниже.
Может быть, рассмотренный вариант решения вопросов линейного раскроя и не «высший пилотаж», но однозначно шаг вперед по сравнению с «традиционным» подходом на многих производствах.
Использование надстройки MS Excel «Поиск решения» (Solver) было на блоге уже однажды рассмотрено в статье «Бак для воды? «Поиск решения» в Excel!». Думаю, что этот замечательный инструмент достоин пристального внимания и еще не раз поможет изящно и быстро решить ряд новых нетривиальных задач.
P.S. Ссылки на лучшие из бесплатных программ линейного раскроя, найденных мной в Сети:
http://stroymaterial-buy.ru/raschet/70-raskroy-lineynih-izdeliy.html
http://forum-okna.ru/index.php?app=core&module=attach§ion=attach &attach_id=7508
Программы по первым двум ссылкам решают рассмотренную задачу, используя 94 заготовки. Первая программа на других тестах показала чуть лучшие результаты, чем вторая.
http://forum.dwg.ru/attachment.php?attachmentid=114501&d=13823277 74
http://www.planetcalc.ru/917/
Программы по последним двум ссылкам реализуют жадные эвристики и выполняют линейный раскрой в задаче из статьи, используя аж целых 103 заготовки. Применение жадных алгоритмов оправдано в случаях необходимости снижения общего времени операции резки при слишком большом количестве вариантов раскроев в более оптимальных планах.
P. S. (11.06.2019)
В статье «Программа для раскроя в Excel и Calc» представлено решение автоматизации заполнения вариантов (схем) раскроев. Для поиска оптимального плана раскроя кроме надстройки Excel Solver использованы более мощные инструменты: NLPSolver и OpenSolver.
Статьи с близкой тематикой
Отзывы
49 комментариев на «Линейный раскрой в Excel»
Ваш отзыв
Интересная тема, Александр.
В работе часто пригождается. с радостью изучу.
Прекрасная работа, спасибо!
SVAI-PLUS.COM
Спасибо! Очень интересно!
Александр, Вы как всегда толково решили нужную практическую задачу. Я видел готовые программы для этой цели, но в Excel удобнее, т.к. единая среда для многих расчетов.
Тема линейного раскроя достаточно интересная, для себя решил двумя способами:
1. Использование линейного программирования. Способ аналогичен тому, что здесь описан и является самым эффективным.
Разбивается на два этапа: генерация рациональных (оптимальных по Паретто) схем раскроя, и дальнейшее построение модели и ее решение целочисленным симплекс методом.
Можно использовать заготовки разного размера с ограничением или без ограничения их количества.
При этом основной упор делается при прочих равных условиях на максимизацию «полезного» остатка.
2й способ — решение как частный случай «задачи о рюкзаке» («сумма подмножеств»), в случае когда рюкзаков много. В основе решения динамическое программирование.
Первый способ очень эффективен и позволяет найти наилучшее решение. Но при большом размере заготовки и большой вариативности и малых размерах деталей получается огромное количество схем раскроя. Обойти ограничение в 200 ячеек можно используя альтернативные библиотеки для решения задач линейного программирования.
При большом размере заготовки и малом у деталей, когда невозможно применить линейное программирование из за большого количества схем раскроя, 2й способ отлично справляется.
MichaelCH, спасибо за развернутый комментарий, подсказывающий ищущим ответ правильное направление. Интересно, что я тоже пришел именно к этим двум способам решения задачи линейного раскроя после изучения темы.
Так как это было достаточно давно, то сегодня было бы интересно разобраться с возможностями и сферой применения «новых» алгоритмов — «генетического» и «муравьиной колонии».
Относительно «генетического» и «муравьиного» алгоритма.
Сам не изучал и не применял эти методы для задачи линейного раскроя.
Связывался с разработчиками оконных программ, где необходимо использовать одномерный и двухмерный (гильотинный) раскрой.
«Генетический» алгоритм хорошо себя зарекомендовал для двухмерного раскроя. Думаю, что другого эффективного метода для 2D-раскроя не найти (полный перебор не применим на практике). Раскрой будет зависеть на сколько качественно реализованы мутации.
Для одномерного раскроя «генетический» алгоритм находит результат как правило не лучше, чем можно найти динамическим программированием за тоже время.
PS. Александр, а Вы используете на практике линейный раскрой? Хочу предложить сравнить разные алгоритмы на реальных данных.
Относительно раскроя указанных данных.
Их можно раскроить используя 93 заготовки.
Вариант 1. Максимизация полезного остатка:
330*2 + 270 + 190*3 = 1500 (42 повторения), остаток — 0
330*2 +270*3 = 1470 (32 повторения), остаток — 30
270*4 + 190*2 = 1460 (17 повторений), остаток — 40
330*3 + 190*2 = 1370 (1 повторение), остаток — 130
190 = 190 (1 повторение), остаток — 1310
Использовано 5 различных вариантов схем раскроя, удалось сохранить полезный остаток размером 1310мм
отходы (за вычетом полезного остатка) составили 0*42 + 30*32 + 40*17 + 130 = 1770мм, что составляет 1,27% от размера заготовок
Вариант 2. Минимизация количества переходов:
330*2 + 270 + 190*3 = 1500 (27 повторений), остаток — 0
270*2 + 190*5 = 1490 (17 повторений), остаток — 10
330*2 + 270*3 = 1470 (49 повторений), остаток — 30
В результате получилось деталей чуть больше, чем требовалось:
330мм — 152шт (+1)
270мм — 208шт (+2)
190мм — 166шт (+3)
При этом используется всего три различных варианта раскроя.
Да, чем меньше переходов, безусловно, тем лучше... Оба, предложенных Вами варианта, хороши! Думаю, их можно получить, используя описанный в статье метод, добавив иррациональные на первый взгляд раскрои и введя дополнительные ограничения. Конечно, при по-заказном производстве изготовление лишних деталей — это плохо, а вот получение делового остатка всего лишь в единственном экземпляре вместо металлолома — это здорово! Каким путем Вы получили представленные варианты решений?
PS: MichaelCH, мы используем, хотя и нерегулярно, линейный раскрой. Предложение по сравнению алгоритмов, конечно, принимается.
Решение получил собственной реализацией задачи раскроя линейным программированием. Максимизация «полезного» остатка заложено в алгоритме.
Снижение различных вариантов схем раскроя можно достичь за счет многократных генераций раскроев и выбора наиболее лучшего. Данный процесс также автоматизирован.
С другой стороны, какая разница получаются ли дополнительные детали или нет.
Общее кол-во заготовок — 93шт, суммарный размер всех заготовок — 93*1500 = 139500мм
необходимо получить детали: 330*151 + 270*206 + 190*163 = 136420мм
общие отходы составят 139500-136420 = 3080мм или 2,21% (3080/139500 = 0,0221)
В разных производствах по разному относятся к отходам и переналадке.
В оконном производстве (и аналогичных) переналадка оборудования не важна, больше упор делается на сохранение «полезного» остатка, который можно использовать в дальнейшем.
А, например, при раскрое рулонов пленки, уже не так важно, получаются ли остатки, все обрезки являются отходом. Важным фактором является именно переналадка (перестановка ножей), т.к. эта процедуры достаточно трудоемкая.
Смогу подробнее ответить на Ваши вопросы по скайпу или почте (m-ch собака mail.ru)
Добрый день
оптимальный линейный раскройный план как получить визуально картинкой
Спасибо
Картинку раскроя можно нарисовать в любом графическом редакторе или CAD-программе. Можно нарисовать и в Excel. (И не такое люди рисуют!!!).
А можно полуавтоматически, используя столбчатые диаграммы Excel, настроить и вывести раскройный план в виде диаграммы. (Пример использования столбчатых диаграмм, и еще пример.)
Спасибо за ответ
теперь ясно
Выложил демо-версию своей программы: excelworld.ru/forum/3-21304-1
А вы бы могли привести пример решения в Excel e задачки из книги Синдром стога сена Голдратта?
(astraraskroy.ru)
Кому интересно — почитайте у Сергея Викторовича Багузина:
baguzin.ru/wp/wp-content/uploads/2013/09/Э.Голдратт. -Синдром-стога-сена.pdf
Авторам вопроса, я думаю, ответ не нужен.
«forum.dwg.ru/attachment.php?attachmentid=114501&d=13823277 74»
этот надо контролировать — тестировал его ранее, выдает при большом количестве деталей глюки: повторные строки и т.п.
Спасибо за информацию, Алексей.
В файле RASKROY_GRUPP.xls используется «жадный» алгоритм, который крайне не эффективный на большом количестве деталей
Спасибо. Полезно, понятно. Борис.
Ищу программу по оптимальному раскрою арматуры длиной 6 м, чтобы не считать вручную. Хочу попробовать ваш вариант
Попробуйте.
Спасибо, что поделились — решаю задачу с целью минимизации материала и реза при модернизации теплицы, надеюсь поможет :)
Спасибо
Здравейте,
аз Ви поздравявам за Вашият труд. Это означало подчеркивать число в колоне H.
Поздравьте,
Цветомир Ценов
Спасибо
Добрый день! Мы хотим приобрести программный продукт по раскрою линейного металла. Так же при необходимости, нам важно что бы можно было доработать продукт под наши нужды (дизайн)
Спасибо за статью, но считаю Excel — малопригодный инструмент для программирования серьезных задач.
Есть готовое профессионально исполненное решение для кроя и стыковки металлопроката.
Чем Excel с сотнями встроенных функций и языком VBA «малопригодней» любой другой среды программирования?
А профессиональные решения в виде оформленных прикладных программ, конечно, есть — и платные, и даже бесплатные, и в том же Excel. Правда, результаты расчетов по ним не всегда являются лучшими решениями задач.
Вот именно, что с сотнями, да еще с формулами на листах, которые «испортить» — как два пальца.
А насчет точности — это зависит от количества раскраиваемых деталей — у меня в среднем выходит 1,5-2,0 %, что вполне даже приемлемо и даже больше.
Но раз нет желания хотя бы ознакомиться, желаю и дальше пребывать в счастливом неведении. :)
andris, почему Вы решили, что «нет желания хотя бы ознакомиться»? Пожелания зачем-то пишите про «счастливое неведение»... Не я, Вы же первый ко мне обратились с известием о «малопригодном Excele» и о создании «профессионально исполненного решения».
Где можно посмотреть, ознакомиться с примененным алгоритмом, возможно протестировать Вашу программу?
Точность 1,5-2,0% — это с каким решением сравнение? Или это среднее количество отходов?
Здравствуйте!
Вы первый, кто программирует в среде Excel проявили кажется неподдельный интерес.
На форумах, где сидят большие, как они себя считают «спецы» в Excel, шарахаются от предложений как черт от ладана.
И причина очевидна — боятся, что в их царстве-госудуарстве и на тронах, на которых эти «спецы» восседают, кто-то может подпилить ножки этим тронам.
И больно смотреть, как мучаются потом пользователи с их шедеврами в процессе их практического применения.
Но ближе «к телу».
Я могу выложить где-нибудь на обменнике демонстрационную версию, например, на Yandex.
Приложение работает в среде MS Access и поэтому хотелось бы предварительно знать, в какой версии офиса вы работаете.
Если это Office 2010 и выше, то будет одна версия. Если Office 2003 (не удивляйтесь — многие еще и на нем работают), то это другая версия.
И еще. Прошу извинить за то, что, может быть, был слишком резок в предыдущем послании.
Уж очень меня спецы по Excel «достали»!
Добрый день, andris.
Форумы по этой теме раньше читал, но не участвовал в обсуждениях...
У меня на данный момент MS Access 2007.
Задачу эту для себя я давно решил, закрыл, и интерес, честно говоря, к теме утратил. Остался лишь чисто математический интерес к алгоритмам решения подобных задач. Какой алгоритм использован Вами?
Не очень понимаю — что я должен увидеть в демоверсии? Если Вы решили продавать (продвигать) программу, то чем я могу быть полезен в этом деле?
Ну, если интерес к этой теме потерян, стоит ли затевать демонстрацию?
Я конечно не настолько наивен, что вы решитесь приобрести это приложение.
Просто случайно по поисковику наткнулся на ваш сайт и решился написать.
Во-вторых, данная задача решалась в основном для строительных организаций и предприятий, выпускающие металлоконструкции, на одном из которых я работаю.
По производственной необходимости у меня накопилось довольно много разработок, облегчающие жизнь офисным работникам и инженерному персоналу производственных цехов. В настоящее время, объединив эти задачи в один комплекс и логически связав их, получилась мини ERP-система. Руководители очень довольны, что наконец-то беспорядочный хаос в документообороте, который царил на заводе, наконец-то, начал приобретать системный характер.
Не скрою, конечно же, есть желание «монетизировать» эти разработки, но подходящей платформы (информационного ресурса) для этого пока нет.
Если будет время, наверно придется самому создать какой-нибудь сайт. Только сомневаюсь, будет ли от этого положительный «выхлоп» и насколько это целесообразно.
Как всегда, на все не хватает времени. И на этом, разрешите откланяться.
Удачи и успехов, andris!
Дважды заданный вопрос о названии примененного алгоритма решения задачи так и остался без ответа...
andris, у меня есть огромный интерес к математической реализации алгоритма линейного раскроя.
Хотелось бы понять, каким алгоритмом Вы делаете раскрой?
Какой получается результат с точки зрения отходов?
Есть ли оптимизации по сокращению вариантов различных схем раскроя, максимизации полезного остатки, минимизации отходов и др.?
Среда разработки вторична, в Excel, Access, C++ не принципиально.
Выложите примеры полученных раскроев, либо я могу предоставить тестовые данные
Ответ Михаил Ч.
Re> Выложите примеры полученных раскроев, либо я могу предоставить тестовые данные
Для начала неплохо было бы ваш e-mail хотя бы.
Я не знаю, разрешает ли этот сайт обмениваться адресами.
Re> Есть ли оптимизации по сокращению вариантов различных схем раскроя, максимизации полезного остатки, минимизации отходов и др.?
Оптимизация идет по 2 критериям: минимум отходов, и максимальная длина полезного остатка
То, что это только линейный раскрой, вы наверно уже поняли?
andris, Михаил Ч, можете здесь обменяться адресами. Или с вашего обоюдного согласия могу отправить вам ваши e-mail. Если напишите их в комментариях здесь, могу через какое-то время удалить по первому вашему требованию.
>>Для начала неплохо было бы ваш e-mail хотя бы.
m-ch собака mail.ru
andris, можно выложить результаты раскроя и на Яндекс диск или другой файлообменник
Например, для тестовых данных задачи раскроя из Википедии:
Размер/Кол-во
1380 — 22
1520 — 25
1560 — 12
1710 — 14
1820 — 18
1880 — 18
1930 — 20
2000 — 10
2050 — 12
2100 — 14
2140 — 16
2150 — 18
2200 — 20
При размере заготовки 5600, размере пилы = 0, торцевой кромке = 0
Можно получить раскрой в 73 заготовки.
Какой получается раскрой Вашей программой?
Можете приложить результаты раскроя и сообщить каким алгоритмом происходит раскрой?
Здравствуйте!
Результат кроя выложил здесь
yadi.sk/i/0hW9E8EFcP-zVw
Александр, спасибо за помощь- за адрес.
На форумах подобное карается. Видимо боятся, что кто-то мимо них кассу пронесет :)
andris, почему Вы упорно не хотитите ответить на вопрос о примененном алгоритме?
Косвенно по предоставленному Вами результату решения задачи раскроя из Википедии (75 заготовок) могу лишь предположить, что примененный Вами алгоритм не находит лучшее решение задачи — 73 заготовки, в отличие от программы Михаила Ч. и моей бесплатной программы в Excel или Calc, размещенной на этом сайте. И количество схем раскроя в Вашем плане раскроя — 14 (лучшее решение — 10)...
Здравствуйте!
Я ни с кем не соревнуюсь в академическом споре, какой алгоритм математически более точен и чем он лучше.
Я — практик и наше предприятие вполне устраивает предложенный мною вариант. И даже более того, экономия металла свелась к небывалым ранее показателям.
«Ловить блох» — себе дороже — так считаю не я, а моё руководство.
А насчет алгоритма, если честно, я не могу представить как мне его расписывать здесь.
Представлять это в виде формул у меня нет времени на это. Да и математика уже давно подзабылась.
Выкладывать код программы — это кормить разного рода «халявщиков», чем я не собираюсь заниматься. Не из-за жадности моей, а ради знаний, которые должны добываться потом и кровью, а не с помощью Google.
andris,
>>А насчет алгоритма, если честно, я не могу представить как мне его расписывать здесь.
Один из моих алгоритмов, построенный на решении задачи «Сумма подмножеств» можно описать следующим образом:
Берете брусок и находите вариант его оптимального распила (чтобы минимизировать остаток). Это задача о рюкзаке или сумма подмножеств. Распиливаете брусок, перерассчитываете количество еще не сделанных деталей. Опять берете брусок, находите его оптимальный распил с использованием еще не сделанных деталей, ... и т.д., пока не будут получены все детали. Если есть остатки, то процедуру начинать с самого короткого бруска.
Данный способ в большинстве случаев дает результат лучше чем «жадный» алгоритм, но тоже не гарантирует оптимальное решение. Рационально данную задачу решать динамическим программированием. Для улучшения результата можно производить сортировки и перемешивание деталей и многократно производить решение, после чего выбрать наилучший результат из имеющихся решений.
Поэтому и спрашивали, как решали? Через линейное программирование, генетическими алгоритмами, полным перебором, жадным алгоритмом, частичным перебором с эвристиками и т.п.?
>>экономия металла свелась к небывалым ранее показателям
А если можно сделать еще лучше?
Если даже на одном крое можно сократить требуемые заготовки на несколько единиц, то это уже окупит вложения в программное обеспечение и в разработку эффективного алгоритма.
Вот примеры данных, которые раскроены достаточно оптимально с точки зрения количества использованных заготовок и сохранения «полезного» остатка: yadi.sk/d/4MnxWi4tDvceWQ
Сможете сравнить раскрой с результатами своей программы
Очень странно получается. У меня ексель 365 и внем немного настройки поиска решений выгледят по другому немного, но в целом похожи и стоят по умолчанию со скачаного файла, но тем не менее когда я произвожу поиск решений, не смотря на ограничение, что расчетное количество =целое у меня значения выходят дробные. С чем это может быть связано?
Это происходит в файле вашем, который я скачал
Не знаю. Попробуйте поменять настройки параметров поиска решения.